Calculate PI by measuring the area of a circle in JavaScript
Introduction
This is a fun little JavaScript program that you can implement on your own or together with young coders at a coding club or at home.
Math
The approximative value of π is known since the times of Archimedes. Over the years many mathematicians and researchers were preoccupied with calculating the value of PI with a higher and higher precision. Lots of new methods have been found to calculate the value of this intriguing number.
Knowing π is very important as its value is used in many mathematical applications. Probably the most well-known applications are determining the circumference and area of a circle of known radius.
In this article we will attempt to calculate the approximative value of π using a method that even a middle schooler will understand - we will measure manually the area of a circle and then work in reverse to determine π.
We know from the math class that area of a circle is:
A = πr²
We usually solve this equation for area or radius. But this time we will solve the equation for π.
π = A / r²
Algorithm
To solve this equation, we will use an empirical method with the help of JavaScript. The method is quite simple:
- Step 1: Assume a circle of radius r
- Step 2: Enclose the circle in a tight square. The square will have sides equal to the diameter of the circle
- Step 3: Determine the area of the circle by counting all pixels that are inside the circle
- Step 4: Determine π by dividing the area to the radius squared, like in the formula above
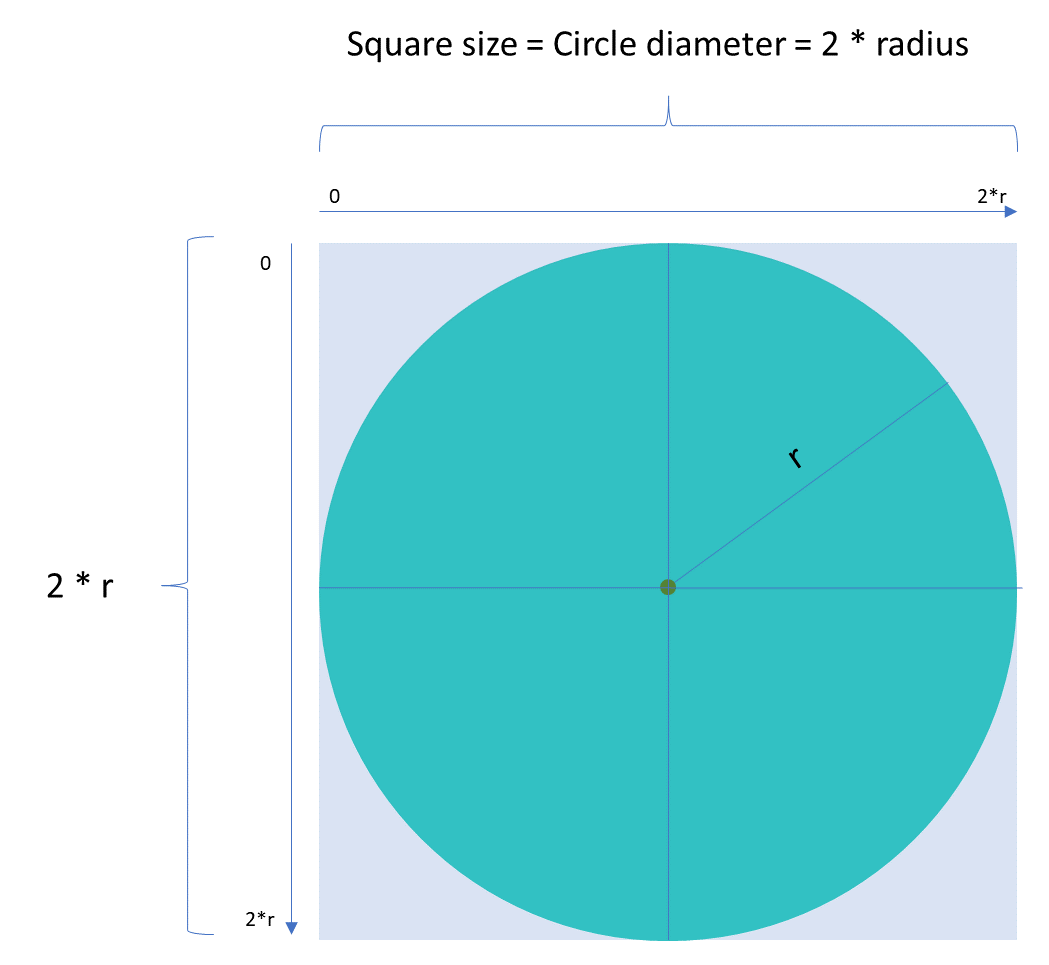
Challenge 1. As you can see the algorithm is simple, but the first challenge already appeared. At step #3 we said that when we need to determine if a point is inside the circle or not.
In order to do this, we will scan all the points inside the outer square and determine if that point is inside the circle or not. This is achieved by comparing the radius of the circle with the distance from that particular point to the center of the circle.
If the distance is smaller or equal than the radius, then the point is inside the circle.
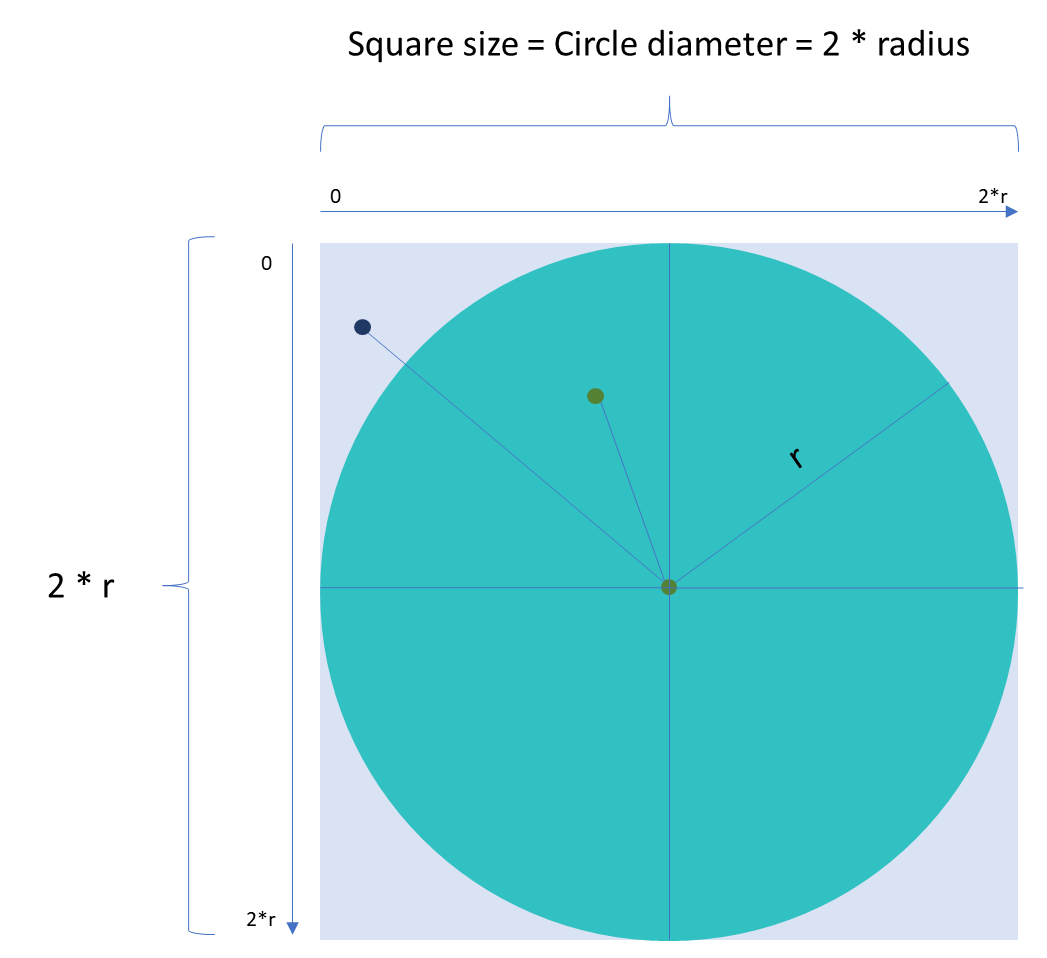
Since this is an empirical method, we will try to improve the precision of the calculations by using a large enough circle. Using a circle with a small radius may result in less precise π approximation due to a less than ideal circle. See the following image:
![]()
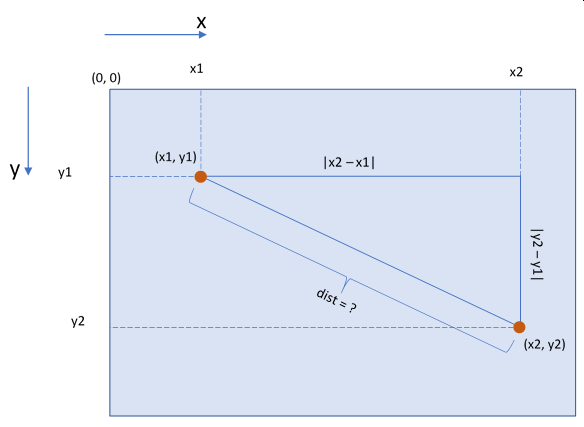
Challenge 2. The previous challenge raised a new challenge on its own. How do we determine the distance between two points?
The answer is: with the help of a little bit of geometry knowledge and Pythagorean theorem.
Since we know the coordinates of the two points, we can determine the triangle sides and then find the hypotenuse using the theorem of Pythagoras.
The following image should be self-explanatory for this.
Now we have all the data we need to start writing the JavaScript code that will calculate π.
You can use any JavaScript environment or playground to write the code. In this article we will use the free codeguppy.com environment (go ahead and create a free account -- you'll have fun).
Although we talked until now only about graphical concepts, the code won’t use any graphical library. We can implement this algorithm using only pure JavaScript without drawing circles or squares.
var p = calcPI();
println(p);
function calcPI()
{
// Choose an arbitrary circle radius
var r = 100;
var diameter = r * 2;
var area = 0;
// Scan all the pixels inside the square
for(var x = 0; x < diameter; x++)
{
for(var y = 0; y < diameter; y++)
{
// Calculate the distance from each pixel
// to the center of the circle
var d = dist(x, y, r, r);
if (d <= r)
{
// If distance is less than the radius
// then add it to the area of the circle
area++;
}
}
}
// Calculate PI by dividing the area to the
return area / (r * r);
}
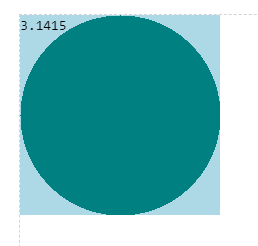
If you copy the above code in the codeguppy.com editor and run it, you will see the result displayed:
3.1415
This is pretty accurate for such simple empirical method!
Note: Please notice that we didn’t defined the dist function that calculates the distance between two points. This is because this function is already defined in codeguppy.com. However, if you want to run the code outside codeguppy.com, then you can easily implement this function in just a few lines of code as explained above. We will leave the exercise of dist function implementation to the interested readers.
Visualizing the circle
As you saw there is no need to use any graphical library to calculate the π using this method. However, since we are in a graphical environment, let’s have a little bit of fun and visualize the points that we are scanning.
We will use the point function to plot the scanned point in either “teal” (if is inside the circle), or “lightblue” if is outside the circle.
Just add the following stroke() and point() lines in the right place:
...
if (d <= r)
{
// If distance is less than the radius
// then add it to the area of the circle
area++;
stroke("teal");
}
else
{
stroke("lightblue");
}
point(x, y);
...
And this is the execution effect:
I hope you had fun with this JavaScript math exploration!
You can find a working example of this code in this playground: code.html?Z25MRrzMBK8zRwDaeaZY
Happy coding and don't forge to share with us or on social media about your coding experience!
Read more blog articles Browse JavaScript projectsAbout codeguppy
CodeGuppy is a FREE coding platform for schools and independent learners. If you don't have yet an account with codeguppy.com, you can start by visiting the registration page and sign-up for a free account. Registered users can access tons of fun projects!

Follow @codeguppy on Twitter for coding tips and news about codeguppy platform. For more information, please feel free to contact us.
